今天这个设计算法,我们先称它为“大力出奇迹 Design Algorithm”,不介意的话,你也可以叫它计算图形学(computational graphics),它能让你复刻所有人类设计大师,甚至早于未来设计大师复刻未来的设计大师。
假设我们需要在一个1000×1000 像素的图片上创作一个纯黑白的图形(如 icon),那么翻译成更严苛和理性的语言就是,我们有1,000×1,000=1,000,000 个点,这些点可以是黑或白两种颜色。如果我们穷尽这个1000×1000上面的所有黑白点的组合可能,我们就会有 2^1,000,000 种可能性,那么,诸如我们熟悉的 耐克、麦当劳、奔驰等等logo的黑白图稿,一定会出现在这个 2^1,000,000 中。
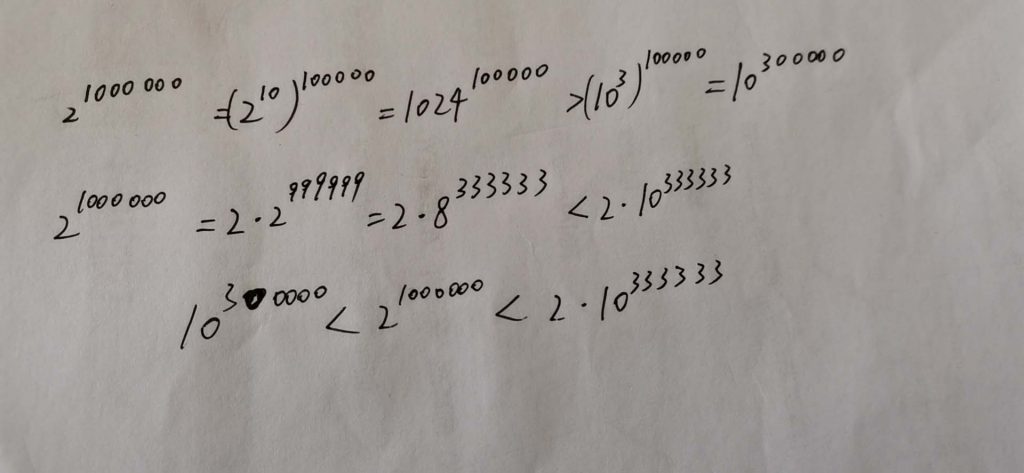
图·不愿透露姓名的数学博士手稿
根据我一位数学博士的“缩放法”的大致定义,2^1,000,000表现成10进制的数字大约是:一个后面跟着30万-33万个零的超长数字串。如果你一秒钟可以画10个图形,那么画完你需要的时间比目前大爆炸理论下宇宙的寿命还多不知道多少倍,数量级都差了10^不知道多少个次方。
那么,如果我们人类的算力足够夯,我们“大力出奇迹 Design Algorithm ”用强大的算力穷举出所有平面图形可能性的可能性确实是存在的。并且理论上讲,“大力出奇迹”算法确实可以复刻人类所有设计师目前的设计精华,并且创造出未来人们迟早会创作出的新设计,设想一下2321年的人看到2021年的人穷举出的2121年经典设计将是怎样一种风味。设想一下,穷举出人类所有的图形可能性(无论它有多少)是怎样一种恐怖,再新颖的设计师都无法在1000×1000的画面中创造出新图形了。
横向对比一下,有点像刘慈欣笔下的“降维”,也有点像物理上的“省力不省功”,我们把“设计这件事”通过算法分解成了极度简单却极多的事情。
而如果我们更加雄心壮志,不满足于黑白而创作彩色,以RGB(0-255)为范围的话,那么每个点的变量可能性就成了 (256^3),而整体画面的可能性就会陡增至 (256^3)^1,000,000 ,我已经失去了在脑中给这个数字以形象和感性理解的能力。但至少理论上我们掌握了一个不高的分辨率情况下人类所有可能的平面画面。
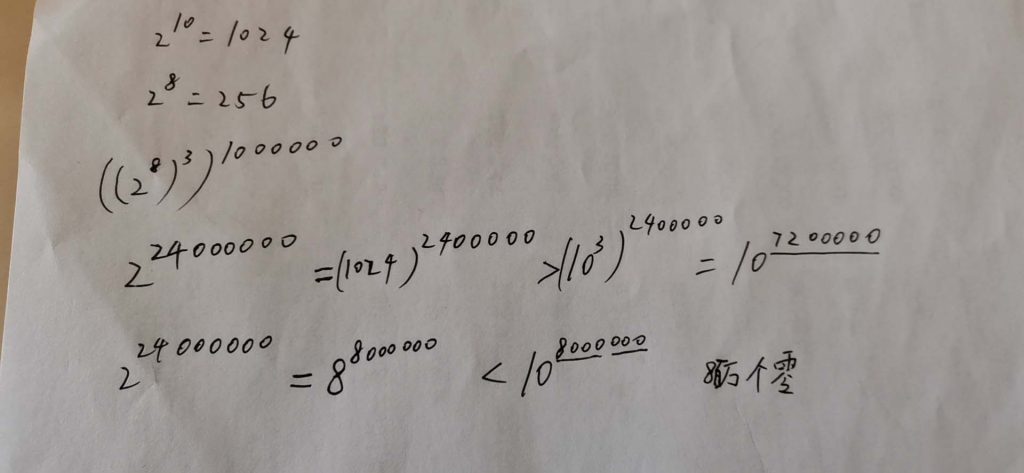
图·不愿透露姓名的数学博士手稿
根据我一位数学博士的“缩放法”的大致定义, (256^3)^1,000,000 表现成10进制的数字大约是:一个后面跟着700万-800万个零的超长数字串。如果你一秒钟可以画10个图形,那么画完你需要的时间比目前大爆炸理论下宇宙的寿命还多不知道多少倍,数量级都差了10^不知道多少个次方。
那么,而在不考虑画幅比例和RGB色域的表现力局限的情况下,如果我们人类的算力足够夯,我们“大力出奇迹”Design Algorithm 用强大的算力穷举出所有平面彩色图形可能性的可能性确实是存在的。并且理论上讲,“大力出奇迹”算法确实可以能复刻出梵高、复刻出达芬奇,创作出未来画家还没画出的画,甚至得到几十年后你的子孙的肖像画。前提是,你可以从 (256^3)^1,000,000 中找到你要的画面。
回到话题上,除了像喝多了一样痴人说梦,聊这玩意有什么用?通过这东西我想说的是,别管执行难度有多高,起码 theoretically 设计的难度(complexity) 是可以被转化为简单的工作量(workload) 的。虽然目前算法上看,算法死在了工作量,这时候,就是修正补偿算法上线的时候了。
设计师所学习的东西,无论身法还是心法,就是通过提高自己工作的复杂程度,在分解设计难度 (complexity) 的时候不至于分解到我们上述的黑白01或RGB 0-255 这样的简单程度上,我们会在一个较高层次上展开我们对于问题的解决,比如我们掌握了构成法则就会砍掉70%(我瞎猜的)不符合构成法则的可能性冗余;比如我们掌握了配色法则就会砍掉70%(我瞎猜的)严重违背人类视觉喜欢的色彩组合可能性冗余,从而一方面以解构问题的形式让复杂性 complexity 变成工作量 workload,而又不至于分解成人不可能承受的工作量。或者说,设计师的身法和心法是对于“大力出奇迹”算法的一种修正补偿算法。
简单说:
complexity = 太难了你不会做
workload = 你会但没有那么多时间
设计的身法心法 = 两者中间找个点
如果上述描述你听懂了,那我们不妨再进行一次升维,比如我们如何能够利用“大力出奇迹 Design Algorithm”复刻出一台保时捷911跑车的造型?
我们定义出一个 1000x1000x1000 的空间,在空间中每个点都可以是有或无,那么,2^(1000x1000x1000)次方的之中,就可以以不高的精度完成人类所有三维形态的尝试和探索了,这其中也自然包含了保时捷911,sounds easy.
如果上述描述你没听懂,那我们这篇文章可以被浓缩为:画图狗赶紧去画图吧,多画图总能撞到好方案的。
那么,本文就到这里,希望给你带来奇妙视角的同时,能引发你的思考。至少,当个段子看看也不错。
致谢:
- 本文基础算法穷举思维受到 《从一到无穷大·科学中的事实和臆测》(作者 乔治·伽莫夫)“第一部分 做做数字游戏”内容启发。这是一本好书推荐给大家。
- 本文数字推算部分受到一位不愿透露姓名的数学博士支持,祝他新婚快乐
文章作者:Natt
教学总监
拉夫堡大学硕士
辅导学生多次录取伦艺/罗德岛/帕森斯/爱丁堡/米理等名校
任何关于院校和作品集的问题
欢迎随时和马克君沟通
知无不言,言无不尽







